이 논문은 ICLR 2023에 출판된 논문이며 Spotlight 논문 (상위 20%) 으로 선정되었다. 저자는 Sumyeong Ahn*, Jongwee Ko*, Seyoung Yun으로 구성되어 있다.
Motivation
기존 연구들은 Class imbalance 문제를 해결하기 위해 주로 rewighting, resampling 기법을 사용했다. Reweighting은 training loss에서 minority class sample의 비중을 크게 하는 방식이며, resampling은 minority class를 더 많이 sampling하거나 majority class를 덜 sampling 하여 균등한 학습 데이터로 재구성하는 방식이다. 하지만 이 방식들은 여전히 한정된 minority class의 정보를 활용한다는 점에서 문제가 있다.
이러한 문제를 해결하기 위해 Data augmentation (DA) 을 활용한 메소드들이 나왔다. Minority sample들을 서로 interpolate 하거나 majority class의 정보를 minority class에 transfer 하는 등 data augmentation 을 활용한 기술이 많이 제안되었지만, class imbalance 문제에서 다른 class들에 대한 data augmentation 강도의 영향을 연구한 work은 거의 없었다. 이 논문에서는 이에 대한 연구를 진행한다.

저자들은 class 별로 augmentation을 진행하는 실험을 했을 때 augmented class에서는 성능 향상이 미미하거나 간혹 떨어지기도 했던 반면, non-augmented class에서 오히려 성능 향상이 있음을 확인하였다. 그 실험은 Figure 1을 통해 확인할 수 있다. 그림에서 빨간 화살표 방향으로의 움직임은 minority class의 augmentation 강도를 늘리는 것을 의미하고 노란 화살표 방향으로의 움직임은 Majority class의 augmentation 강도를 늘리는 것이다. 또한 top row의 그림은 majority class의 accuracy, bottom row의 그림은 minority class의 accuracy를 나타낸다.
그림을 보면 class의 balanced, imbalanced에 상관없이 실험 결과는 비슷한 양상을 보이고 있다: major class에만 강하게 augmentation을 했을 때 majority class의 성능이 떨어지는 반면 minority class에서는 괜찮은 성능을 보인다. 또한 추가적인 실험 (Appendix A)을 통해 data augmentation의 strength 커질수록 weight norm이 작아짐을 확인하였고, 이 때문에 data augmentation을 강한 강도로 적용한 class의 softmax 값이 작아지면서 accuracy 또한 감소하고 결과적으로 위와 같은 양상을 보였을 것이라 추측하였다.
저자들은 위 실험 결과 및 가설을 기반으로 각 class별 적절한 augmentation 강도를 찾아 성능을 향상시키고자 하였다.
Method
○ Data Augmentation (DA) with strength parameter
이 논문에서 DA의 강도 \( s \)에 대한 input 이미지의 augmentation 결과를 \( \mathcal{O}(x;s) \) 로 표기한다.

우선 pre-defined \(K\) augmentation operation이 있다고 가정한다 (예를 들어, Gaussian blur, Rotation, Horizontal flip 등). 여기서 \(s\)개의 augmentation을 uniform distribution으로 추출한 것을 \(\mathcal{O}_{k_1}, \mathcal{O}_{k_2}, \cdots, \mathcal{O}_{k_s} \)라고 한다. 그리고 \(m_{k_i}(s)\)는 \(k_i\) 번째 augmentation의 magnitude이다. 예를 들어 Augmentation ShearX는 augmentation의 범위가 [0, 3]인데 여기에 strength 3을 적용한다고 하면 magnitude \( m_{ShearX}(s) \)는 \((3-0)/30 * s \) 와 같이 계산한다. 여기서 30은 저자들이 정한 level division 이라고 이해하면 될 것 같다. 이렇게 augmentation의 종류와 강도를 정하고 순차적으로 input 이미지에 적용한다.
정리하자면 strength parameter \(s\)가 크면 클수록 해당 이미지에 많은 종류의 data augmentation을 강한 강도로 적용한다는 것이다.
○ Level-of-Learning (LOL)
저자들은 class imbalance 문제를 해결하기 위해 class별로 augmentation의 강도를 달리하고자 하였다. 따라서 매 에폭마다 각 class별로 augmentation level을 계산한다.
계산 방식은 꽤 직관적이다. 현재 augmentation level (level이 높을수록 강한 augmentation을 적용) 에서 모델이 이미 prediction을 잘 하고 있다면 다음 에폭에서는 level을 1 올리고, prediction을 잘 하지 못한다면 다음 에폭에서는 level을 1 낮춘다. 수식으로 살펴보면 살짝 복잡해 보이기는 한데, 디테일이 궁금하지 않다면 아래 설명은 스킵해도 괜찮을 것 같다!


특정 level \(l\)에서 모델이 잘 하고 있는지를 판단하는 과정은 다음과 같다.
우선 Training data에서 class \(c\)의 sample 중 일부를 추출하여 \(\mathcal{D}'_c \)를 구성하고, 이 dataset에 대해 level \(l\)의 augmentation을 적용한 뒤 inference를 진행한다. 이 때 \(\mathcal{D}'_c \)의 size는 \(T(l+1)\)인데 \(T\)는 hyperparameter로 default value는 10이다. Augmentation의 level 별로 LoL value를 계산하기 위한 dataset의 크기를 달리하는 이유는 augmentation level이 커지면 커질수록 가능한 augmentation의 조합의 수가 exponential하게 커지기 때문이다. 현재 모델이 현재 level에서 잘 하고 있는 지를 판단하기 위해서는 \(\mathcal{D}'_c \)가 augmentation space를 잘 커버하고 있어야 하므로 더 많은 양의 데이터를 사용해야 한다. \( V_{Correct} \)는 class c의 \(T(l+1)\)개의 training sample들 중에서 맞은 prediction의 수를 output으로 갖는다.
\( \gamma \)는 [0, 1] 범위 내의 값을 가지는 hyperparameter로 여기서는 threshold 역할을 한다. \( \gamma \)가 0.7이라면 \(\mathcal{D}'_c \)의 70%를 맞춰야 model이 잘 predict하고 있다고 판단한다.
현재 에폭 \(e-1\)에서 class \(c\)에 대한 augmentation level을 \(L_c^{e-1}\)이라고 할 때, level 0부터 level \(L_c^{e-1}\)에 대해 모델이 잘하고 있다는 것이 확인되면 다음 에폭 \(e\)에서 class \(c\)에 대한 augmentation level은 \(L_c^{e-1}\) + 1이, 그렇지 않으면 \(L_c^{e-1}\) - 1이 되는 것이다.
○ Curriculum of DA
CUDA는 위에서 기술한 DA with strength parameter와 LoL을 결합하여 class-wise adaptive augmentation을 제공한다. 매 에폭마다 클래스 별로 적절한 data augmentation의 정도를 계산하고 이를 활용하여 다음 에폭에서 학습을 진행한다. 또한 실제 학습에서는 다른 DA 방식들처럼 비슷하게 확률적으로 augmented sample을 활용한다.

Experiments
실험은 데이터셋 CIFAR-100-LT, ImagNet-LT, iNaturalist 2018 에 대해 진행하였다. CUDA와 비교를 진행할 기존 베이스라인 메소드는 다음과 같다.
- Cross-entropy loss (CE)
- Two-stage approaches (CE-DRW, cRT)
- Balanced loss approaches (LDAM-DRW, Balanced Softmax)
- Ensemble method (RIDE)
- Resampling algorithm (Remix, CMO)
- Constrasitve learning-based approach (BCL)

Table 1은 CIFAR-100-LT에 대해 실험을 진행한 결과이다. CUDA가 결합된 경우 balanced validation (uniform) performance가 향상되었음을 확인할 수 있다.

최근 굉장히 다양한 augmentation 전략과 긴 학습 시간을 사용한 베이스라인 논문들이 좋은 성능을 보이고 있는데, 이러한 기술들에 CUDA를 적용하더라도 성능 향상이 있었다.

Table 2는 ImageNet-LT와 iNaturalist 2018 데이터셋에 대한 실험 결과이다. CUDA는 복잡한 메소드 구조 없이 단순히 class-wise data augmentation을 적용하였음에도 불구하고 일관적으로 성능을 향상시키는 모습을 보이고 있다.
Analysis
○ How does CUDA mitigate the class imbalance problem?
저자들은 CUDA에 대한 깊은 이해를 위해 validation set에 대해 다음의 두 metric을 확인하였다.
(1) 각 class 별 linear classifier의 weight L1-Norm의 분산
(2) 각 class 별 feature alignment gain

Weight norm은 model이 input에 대해 class별로 얼마나 balanced된 예측을 하는지를 측정할 때 많이 사용된다. 위의 그림은 모델의 linear classifier를 나타낸 모습이다. 여기서 input feature와 첫 row를 내적한 값이 class 1의 최종 logit이 되기 때문에 weight의 첫 row는 class 1에 대응되는 weight이라고 볼 수 있다. 마찬가지로 두 번째 row는 class 2에, N 번째 row는 class N에 대응되는 weight이 된다. 만약 첫 row의 L1-norm이 상대적으로 매우 크다면 모델은 대부분의 inference에 대해 class 1의 logit을 크게 만들게 되므로 우리는 이 모델을 class 1에 biased된 model이라고 평가할 수 있다. 따라서 각 class 별 weight norm이 비슷한 모델을 이상적인 모델이라고 생각할 수 있다.
feature alignment는 같은 class 내의 sample들에 대해 feature를 추출했을 때, 그 feature들이 얼마나 align되어 있는지를 계산한 것이다.

Figure 3 top row 에서 볼 수 있듯이 CUDA는 weight norm의 분산을 줄이는 효과를 보이고 있다. 즉, class 별로 weight norm의 차이가 줄어들게끔 하여 모델이 덜 편향된 예측을 하게끔 돕는다. 참고로 여기서 LDAM-DRW와 RIDE는 cosine classifier를 사용하기 때문에 scale이 다르다.
Bottom row는 feature alignment gain에 대한 결과이다. 마찬가지로 CUDA를 사용함으로써 거의 대부분의 class에 대해 feature alignment gain을 얻을 수 있었다. 이는 CUDA가 모델이 보다 meaningful한 feature를 추출할 수 있도록 돕는다는 것을 의미한다.
○ Compared with other augmentations
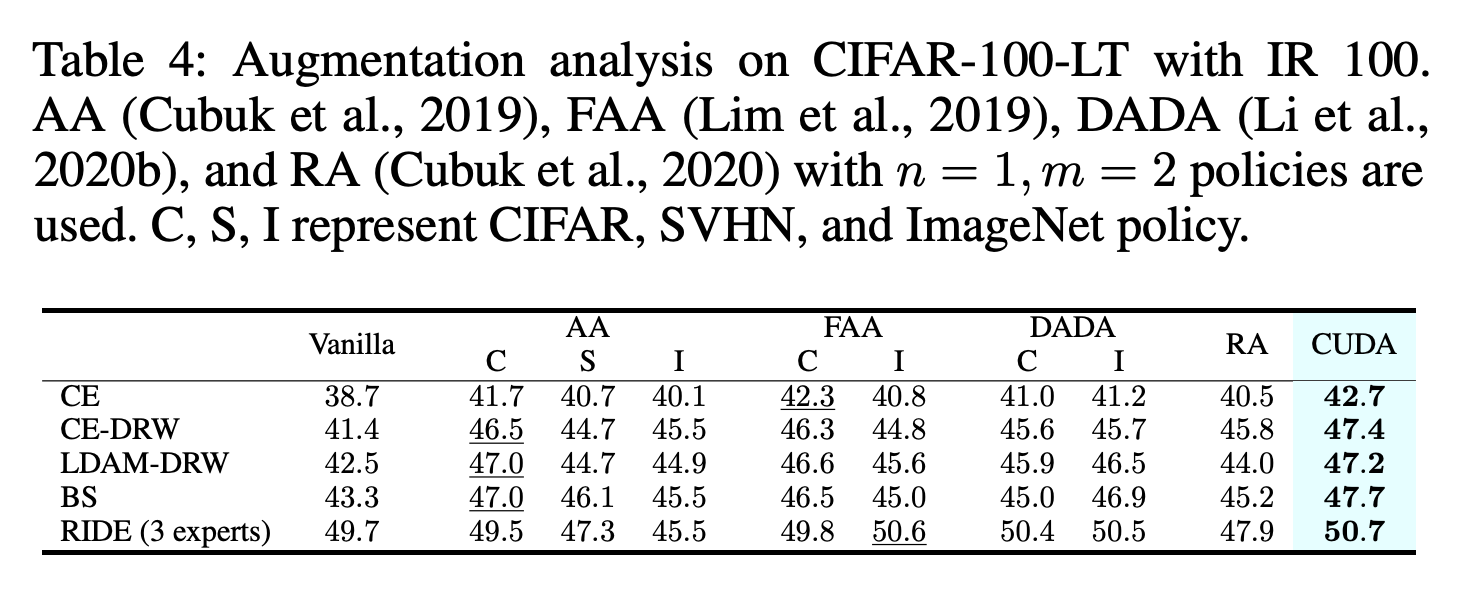
또한 Table 4를 보면 다른 augmentation 기법들과 비교해도 CUDA는 outperform 한다. 베이스라인의 성능은 각 논문에서 제시한 최적의 hyperparameter를 활용한 결과이다. CUDA는 이러한 추가적인 리소스 없이도 pre-searched augmentation보다 더 좋은 성능을 보였다는 점에서 큰 장점이 있다.
○ Dynamics of LoL score

Figure 4는 CUDA를 활용하여 학습함에 따라 LoL score가 어떻게 변화하는지를 관찰한 것이다. 모든 알고리즘에서 학습을 진행할수록 LoL score는 커지는 모습을 보였다. 특히 BS 알고리즘을 제외하고는 상대적으로 majority class에서 LoL score가 가파르게 상승하는 모습을 볼 수 있다. 저자들은 BS에서 majority class와 minority class가 비슷한 LoL score 양상을 보이는 것은 majority와 minority sample들의 영향을 balancing하는 모듈이 있기 때문이라고 주장한다.
○ Parameter sensitivity

Figure 5의 (c)를 보면 \( \gamma \)가 너무 크거나 너무 작으면 성능이 하락하는 것을 볼 수 있다. \( \gamma \)는 모델이 현재 level에서 잘 하고 있는지를 판단할 때 사용하는 threshold인데, 이 값이 너무 크면 level이 항상 낮게 유지되어 augmentation이 계속 약하게 적용된다. 반대로 이 값이 너무 작으면 실질적으로 모델이 예측을 잘 하지 못할 때도 level이 쉽게 높아져 강한 augmentation이 계속 적용된다. 따라서 (c)의 실험 결과는 augmentation이 너무 강하거나 너무 약하면 성능이 하락한다는 것을 의미한다.
그리고 (b)를 살펴보면 \(T\)의 값이 클수록 성능이 향상되는 것을 볼 수 있다. \(T\)는 LoL score를 계산할 때 사용하는 training data의 subset이다. \(T\)가 커질수록 LoL score를 더 많은 데이터셋에서 계산할 수 있게 된다. 하지만 \(T\)를 큰 값으로 정하게 되면 계산량이 많아진다. 저자들은 cost-effective한 성능 향상을 얻기 위해 \(T\)의 default value를 10으로 사용하였다.
○ Impact of curriculum
저자들은 class별 augmentation 강도를 hyperparameter optimization 알고리즘에 기반하여 searching한 경우와도 성능을 비교하였다. 이에 대한 실험 결과는 Figure 5 (d)에 있다. 이 때 curriculum learning의 영향을 분리하여 살펴보기 위해 CUDA w/o Curriculum 에 대한 실험 결과도 함께 report 하였다. CUDA w/o Curriculum은 CUDA를 한 번 학습시킨 뒤 가장 마지막 에폭에서 각 class별 augmentation level을 얻어내고, 이를 적용하여 모델을 re-train함으로써 얻은 결과이다.
CUDA가 찾아낸 class별 augmentation level을 적용했을 때에도 pre-searched baseline과 비슷하거나 더 나은 성능을 보이고 있다. 이는 CUDA가 lower seraching time으로도 더 나은 augmenatation 강도를 찾았음을 의미한다. 게다가 curriculum 방식으로 학습함으로써 CUDA는 추가적인 generalization 성능을 얻을 수 있었다.
Conclusion
- Class imbalance 문제를 해결하기 위해 CUDA라는 새로운 메소드를 제안함
- 기존의 메소드에 쉽게 결합될 수 있는 add-on 메소드임
- CUDA는 추가적인 searching 없이, LoL score를 측정하여 적절한 augmenation 강도를 adative하게 찾아낸다
- CUDA가 여러 데이터셋에서 기존 베이스라인들의 성능을 능가하였음을 보였음
- CUDA가 class balance 문제를 해결하는 효과가 있으며, majority class에 대해서도 도움이 될 수 있는 feature extraction 능력 또한 향상시켰음을 보였음
Data augmentation의 강도는 hyperparameter 라고만 생각했었는데, class 별로 최적의 data augmentation의 정도를 training 과정에서 adaptive하게 찾아낸다는 관점이 굉장히 참신하다고 생각했다.
Data augmentation에서 strength가 성능에 많은 영향을 미치는 것을 보여주고 적절한 hyperparameter의 강도를 학습 과정에서 찾아 적용시키는 메소드를 제시하였다는 점에서 논문의 흐름도 좋았다. 특히나 data augmentation의 강도가 세지면 세질수록 label을 predict하기 어렵다는 것은 꽤 직관적인 내용인데, 여기에 curriculum learning의 철학을 활용하여 논문을 읽는 사람이 직관적으로 메소드를 이해할 수 있도록 글을 작성했다는 점에서도 이 논문을 높이 평가한다.