이 논문은 CVPR 2023에 출판되었으며, 저자는 Jiahao Chen, Bing Su로 구성되어 있다.
Motivation
기존의 calibration 기술들은 대부분 training data가 균등분포를 따른다고 가정하고 있다.

Figure 1에서도 알 수 있듯이, 원래 calibration의 파이프라인은 balanced training set으로 모델을 학습하고, balanced validation set을 활용하여 calibration model을 얻는다. 그리고 target test set은 training/validation set과 동일한 분포를 가진다.
하지만, 실제 real-world에서는 long-tail 분포를 따르는 경우가 많다. 이러한 세팅에서 기존의 calibration 기술들을 사용하면 head class와 tail class에 대한 편향되지 않은 calibration 을 얻기가 어렵다. 예를 들어, validation set으로 부터 얻은 temperature를 사용하는 temperature scaling 방식은 validation set과 test set의 분포가 다를 때 성능 저하가 발생한다. 즉, 이러한 기술은 test set에 잘 generalize될 수 없다는 것이다.
따라서 이 논문에서는 기존 temperature scaling의 generalization 문제를 다루기 위해 knowledge-transferring-based temperature scaling method를 제안한다.
Method
Balanced target distribution \(q(x)\)에 대한 calibration loss는 source distribution \(p(x)\)의 weighted calibration error로 다음과 같이 표현할 수 있다.

위의 식을 보면, target distribution error \( \mathbb{E}_q[\mathcal{L}(s(z_i/T), y_i)] \) 를 각 sample에 대한 probability 비율 \( w(\mathbf{x}) = q(\mathbf{x}) / p(\mathbf{x}) \)를 통해 추정한다. \( p(x_i) \)가 작을수록 importance weight \(w(x_i)\)가 더 크게 반영된다. 하지만 우리는 실제로 \(q(\mathbf{x})\)를 알 수가 없다. 따라서 논문에서는 이 확률분포를 모델링하고자 한다.
우선 long-tailed distribution \(p(x)\)와 \(q(x)\)를 각각 mixtures of Gaussian distribution (MoG)로 모델링한다. 즉, 각 클래스를 Gaussian distribution으로 모델링한다는 것이다.

Figure 3에서 볼 수 있듯이 head class는 \(p(x)\)와 \(q(x)\) 모두 항상 sample을 많이 가지고 있기 때문에, \(q(x)\)에서의 head class distribution은 \(p(x)\)에서의 것과 동일하다고 간주할 수 있다. 반면, tail class는 \(p(x)\)에서 \(q(x)\)에 비해 적은 sample을 가지게 된다. Tail class \(c\)에 대한 distribution \(p_c(x)\)가 sample 수의 부족으로 unreliable하기 때문에, balanced distribution 일 때의 확률 분포를 추정하는 것이 중요하다.
기존 연구들에서도 이야기하고 있듯이 head class와 tail class 사이에 공통된 정보들이 있기 때문에, 저자들은 head class에서 tail class로 정보를 전달하여 balanced distribution을 회복하는 것은 합리적인 방식이라고 주장한다. 더불어 더 비슷한 클래스들끼리 더 많은 정보를 share할 것이라 생각하여, 먼저 class 간의 Wasserstein distance를 측정하였다.

\(\mathbf{d}_c^k\)는 distance vector \(\mathbf{d}_c\)의 k 번째 element로, class c와 head class k 사이의 유사도를 나타낸다. 그리고 attention 메커니즘을 따라, 다음과 같이 attention score \(\mathbf{s}_c\)를 계산한다.

Class \(c\)와 class \(k\)가 비슷할수록 distance \(\mathbf{d}_c^k\)가 줄어들고, \(\mathbf{s}_c^k\)는 커진다. 이렇게 구한 \(\mathbf{s}_c\)를 기반으로 다음과 같이 calibrated distribution을 추정한다. \(\alpha\)는 hyper-parameter이다.

이를 활용하여 tail class의 각 sample \( \mathbf{x}_i \)에 대한 probability \( q^*_{y_i}(\mathbf{x}_i) = \mathcal{N}(\mathbf{x}_i | \mu_{y_i^*}, \sum_{y_i^*}) \)를 얻을 수 있다. 이를 기반으로 다음과 같이 importance weight을 정의한다.

Head class의 경우 두 distribution이 동일하기 때문에 1로 두고, tail class에 대해서는 \( q^*_{y_i}(\mathbf{x_i}) / p_{y_i}(\mathbf{x_i}) \)로 둔다. 이 때, weight이 비정상적인 값이 되지 않도록 최대, 최소값을 각각 \( \eta_1, \eta_2 \) 로 두었다.
이렇게 구한 importance weight을 활용하여 validation set에서 temperature \(T\)를 찾음으로써, training long-tailed distribution과 test balanced distribuiton을 연결한다.

Experiments
실험은 CIFAR-10-LT, MNIST-LT, CIFAR-100-LT, ImageNet-LT 에 대해 진행했다. 각 데이터셋에 대해 training set과 validation set을 80:20 비율로 random하게 나누었다.
- CIFAR-10-LT
- Imbalance factor (IF)가 100, 50, 10일 때에 대해 실험 진행
- Test set은 총 4가지: (1) original CIFAR-10 test set, (2) CIFAR-10.1, (3) CIFAR-10.1-C, (4) CIFAR-F
- MNIST-LT
- IF가 100, 50, 10일 때에 대해 실험 진행
- Test set은 총 4가지: (1) original MNIST test set, (2) SVHN, (3) USPS, (4) Digital-S
- CIFAR-100-LT
- IF가 10일 때에 대해 실험 진행
- ImageNet-LT
- long-tailed training set과 balanced validation set을 합친 뒤, CIFAR-10-LT 제작 방식을 따라 long-tailed training set과 long-tailed validation set을 구성

Table 1을 보면 calibration metric ECE에 대해서 Ours가 모든 test dataset에 대해 가장 좋은 성능을 보였다. 특히 CIFAR-10.1과 CIFAR-F는 real-world로부터 수집된 데이터이기 때문에 이 데이터셋에 대해 좋은 성능을 보인다는 것은 Ours가 다른 domain에 대해서도 generalization이 잘 된다는 것을 의미한다고 주장한다.

일부 경우를 제외하고 MNIST-LT에 대해서도 Ours는 뛰어난 성능을 보인다. SOTA가 아닌 경우에서도 Ours는 충분히 acceptable한 성능을 보인다.
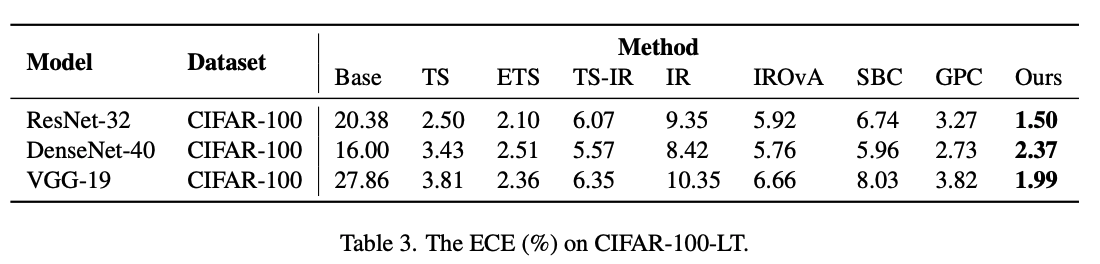
CIFAR-100-LT 벤치마크에서도 Ours가 가장 좋은 성능을 보였다. 또한 여러가지 아키텍처에 대해서 실험을 진행하였는데 ResNet을 사용하였을 때 가장 작은 ECE 값을 얻었다.

또한 이 메소드는 ImageNet-LT에서도 가장 좋은 성능을 보이고 있다. 이를 통해 메소드가 큰 스케일의 데이터셋에서도 유효하다고 볼 수 있다.
Ablation study
○ Reliability diagram
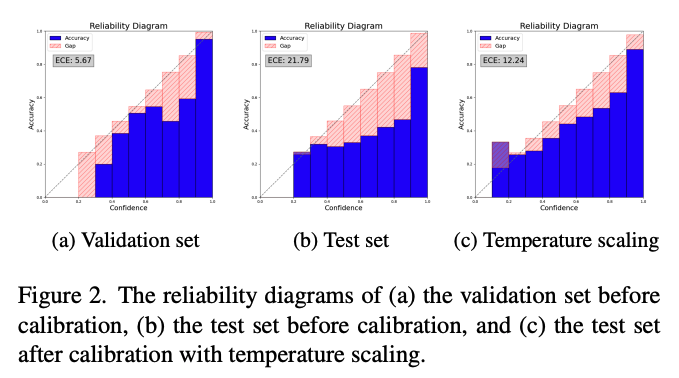
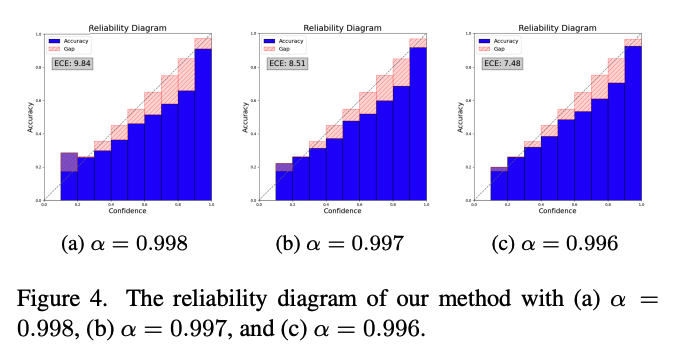
Figure 2는 baseline과 temperature scaling 방식의 reliability diagram이며, Figure 4는 논문의 메소드를 적용한 reliability diagram을 나타낸다. 우선, 이를 통해 논문에서 제시한 메소드가 조금 더 reliable한 calibration 결과를 만든다는 것을 확인할 수 있다.
○ The visualization of attentions
논문의 메소드는 서로 다른 distribution 간의 distance를 계산하고, 이를 통해 attention score를 얻는다.
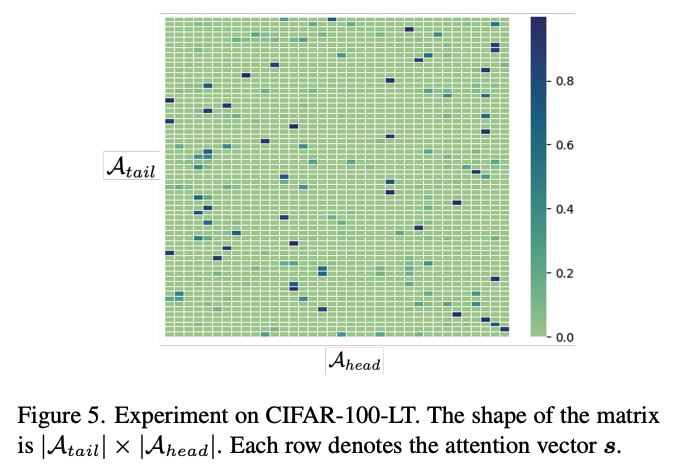
Figure 5을 알 수 있듯이, 각 tail class는 몇 개의 유사한 head class를 보이고 있다. Tail class는 이 유사한 head class의 정보를 사용하게 된다. 예를 들어, tail class "woman"의 유사한 head class는 "boy", "girl", 유사하지 않은 class는 "cloud", "castle"이다. 따라서 "boy"와 "girl" class에 공통 정보가 많을 것이고, 그 정보를 활용하여 "woman"을 학습하는 것이 합리적이라는 것이 저자들의 주장이다.
또한 두 가지 방식의 knowledge transfer 전략을 추가적으로 실험했다.
- OneHot 전략: 가장 유사한 head class 하나에 대한 정보만 활용하고 나머지 class의 정보는 제거
- Uniform 전략: 모든 class에 대해 동일한 비율로 정보를 반영
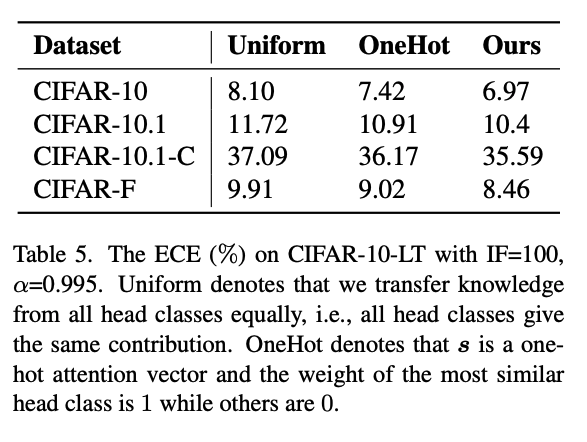
위의 실험 결과를 통해 head class 간의 유사도, 관계성에 따라 중요도를 매기고 이를 기반으로 모든 head class를 학습하는 Ours의 전략의 효과성을 확인할 수 있다.
○ The distribution of \(w^*(\mathbf{x})\)
이 메소드에서는 \(w^*(\mathbf{x}\)의 값의 영향을 많이 받는다. 따라서 training data의 imbalance ratio가 달라짐에 따른 \(w^*(\mathbf{x}\)의 분포를 확인하였다.
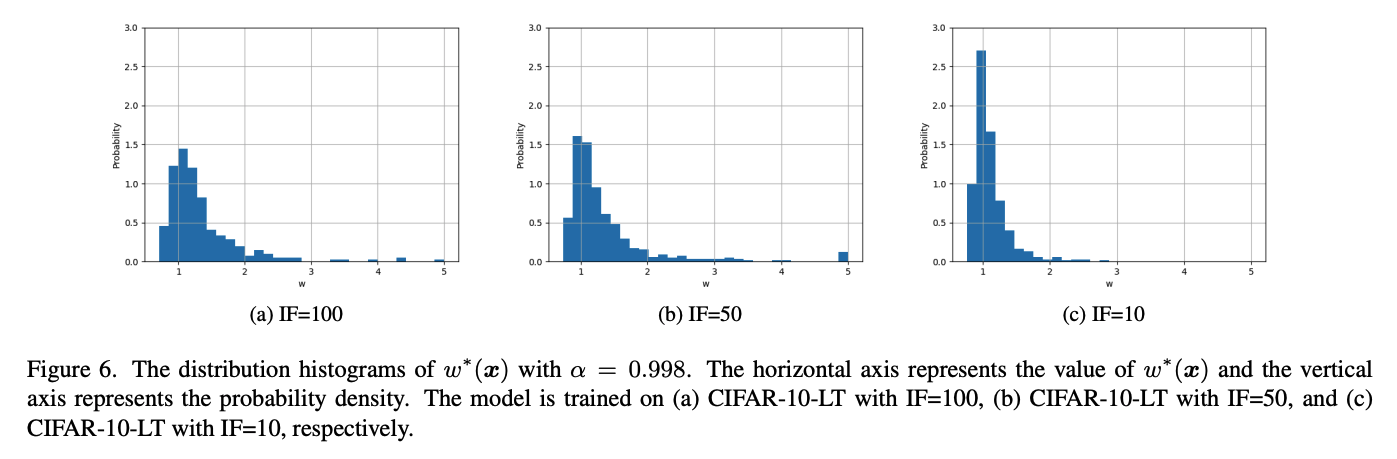
Figure 6을 보면 전반적으로 \(w\)의 분포는 \(w=1\)에 모여있다. 데이터가 더 불균등할수록 \(w\)의 값은 더 커지는 것을 볼 수 있다. 저자들은 이에 대해 IF=100인 데이터셋은 심한 imbalance ratio로 인해 domain shift 문제를 직면하게 되고, 따라서 더 많은 sample들이 큰 \(w\)를 갖게 되는 것이 합리적이라고 주장하였다.
○ Ablation study on hyper-parameter \(\alpha\)
\(\alpha\)는 head class의 정보를 얼마나 transfer 할 것인지를 결정하는 중요한 hyper-parameter이다. \(alpha\)가 작을수록 head class의 정보를 더 많이 사용하는 것이며, \(\alpha=1.0 \)이 경우는 모든 class에 대해 \(w(\mathbf{x}) = 1 \)이 되므로 기존의 temperature scaling 방식과 동일하다고 볼 수 있다.
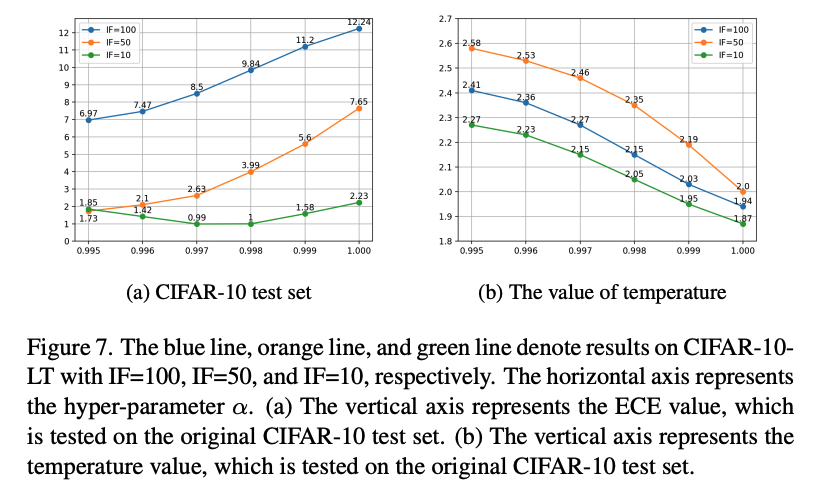
Figure 7의 가로축은 \(\alpha\)의 크기를 나타내며 (a)의 세로축은 ECE, (b)의 세로축은 temperature value를 의미한다. IF=100, 즉 데이터 불균등이 심한 경우에는 \(\alpha = 0.995\)에서 가장 좋은 성능을 보였으며, IF=10에서는 \(\alpha = 0.997\)에서 가장 좋은 성능을 보였다. 이는 tail class의 정보가 적을 때 head class로부터 정보를 더 많이 활용하도록 해야 한다는 것을 의미한다.
특히 (a)에서 초록 line (IF=10)은 \(\alpha < 0.997\)에 대해 다시 성능 저하가 발생하는데, 이는 모델이 underconfident 해지기 때문이라고 한다. 따라서 모든 모델에 대해 단순히 \(\alpha\)를 작게하는 것이 아니라, 불균형 정도에 맞게 \(\alpha\)를 반영해야 한다고 이야기 한다.
Conclusion
- Long-tailed distribution에서의 calibration 문제를 분석
- Head class의 distribution을 tail class distribution의 prior로 활용하여 importance weight estimation method를 제안
- CIFAR-10-LT, CIFAR-100-LT, MNIST-LT, ImageNet-LT에 대해 실험을 진행하여 메소드의 효과성을 입증