이 논문은 CVPR 2020에 출판되었으며, 저자는 KAIST의 Jaehyung Kim*, Jongheon Jeong*, Jinwoo Shin으로 구성되어 있다.
Motivation
기존의 long-tail learning 문제를 해결하기 위한 방법에는 re-weighting, re-sampling 기법이 있다. Reweighting은 loss function에 클래스별 sample 수를 역으로 한 값을 weight으로 반영하여 minority class의 loss를 강조하는 방식이며, resampling은 주어진 데이터셋에서 minority class를 over-sampling하거나 majority class를 under-sampling 하는 방식으로 balanced dataset으로 재구성하여 학습을 하는 방식이다. 이 방식들은 여전히 제한된 minority class의 정보만을 활용하여 새로운 minority sample을 만들어낸다는 문제가 있다. 한정된 정보를 모델에게 계속 학습을 시키기 때문에 overfitting 문제로부터 자유로울 수 없다. 특히 Imbalance의 정도가 매우 커서, minority sample이 매우 적은 경우 성능이 좋지 않다.
이 논문에서는 majority sample을 사용하여 새로운 minority class를 만들어내는 방법을 고안함으로써 위의 문제를 해결하고자 하였다.
Method

M2m은 새로운 balanced dataset \( \mathcal{D}_{bal} \)를 만들어 \(f\)를 학습시키고자 하였다. 이 때, balanced dataset은 다른 majority class의 sample들로 부터 translate된 synthetic minority sample을 추가하여 만든다.
Majority class의 sample을 minority class로 translate 하는 방식은 여러가지 있을 수 있다. Cross-domain generation 연구에서는 generative adversarial network을 활용하여 이와 유사한 결과를 얻을 수 있다. 하지만 이 방식은 training time에서 많은 계산량을 필요로 한다. 따라서 이 논문에서는 간단하면서도 효과적인 방법을 제안한다: Baseline classifier \(g\)에 대해서 target minority confidence를 최대화 하는 방향으로 majority sample을 최적화하는 것이다. 여기서 g는 imbalanced dataset \(\mathcal{D}\)에 대해 pre-training된 또 다른 classifier이다.
○ Sample \(x^*\)을 만드는 optimization problem
Class \(k\)의 새로운 synthetic minority \(x^*\)를 만들기 위해서 상대적으로 major인 class \(k_0\)의 sample \(x_0\)로 부터 e다음의 optimization 문제를 푼다.

\(\mathcal{L}\)은 cross entropy loss를 의미하며 \(\lambda > 0\)은 hyperparameter이다.
이는 간단히 설명하면 majority seed \(x_0\)을 \(x^*\)로 translate 하여, \(g\)가 \(x^*\)를 minority class k로 분류하도록 도모한다. 하지만 여기서 \(f\)가 \(x^*\)를 k로 분류하는 것을 강제하기보다는 \(f\)가 기존의 class \(k_0\)에 대해서 낮은 confidence를 가지도록 제한하는 방식으로 최적화 문제를 구성하였다.
○ Sample rejection criterion
\(g\)의 성능이 좋아야 위와 같은 minority sample generation을 더 잘할 수 있다. \(k_0\)에 대한 feature를 잘 추출해야 generation process에서 \(k_0\)의 중요한 feature를 잘 지울 수 있고, minority class의 sample로 적절히 translate 할 수 있기 때문이다.
하지만 \(g\)는 imbalanced dataset \(D\)에 학습했기 때문에 이상적인 classifier가 아니다. 특히나 \(N_{k_0}\)가 작은 경우 generation 과정을 더욱 신뢰할 수 없다는 문제가 생긴다. 이러한 위험을 완화하기 위하여 저자들은 다음과 같이 간단한 rejecting criterion을 만들었다.

여기서 \((\cdot)^+ := max(\cdot, 0)\)이며, \(\beta \in [0, 1)\)는 \(g\)의 reliability를 조절하는 hyperparameter이다. \(\beta\)가 작을 수록 비교적 적은 \(N_{k_0}\)로도 reject 확률을 작은 값으로 만들 수 있다. 예를 들어, \(\beta = 0.999\)이면 \(N_{k_0} - N_k \gt 4602\)일 때 synthetic data의 accept 확률이 99% 이상이 되고, \(\beta = 0.9999\)이면 \(N_{k_0} - N_k \gt 46049\)일 때서야 accept 확률을 동일한 수준으로 올릴 수 있다는 것이다. 또한 \(N_{k_0}\)보다 \(N_k\)가 더 크다면 k가 더 major class가 되므로 반드시 reject이 되어야 하는데, 이 경우 위의 식을 적용하면 \(\beta^{(negative \; value)^+} = \beta^0 = 1 \)이 되어 이를 만족함을 확인할 수 있다.
새로 만든 \(x^*\)가 위의 criterion에 의해 reject되는 경우 기존의 \(\mathcal{D}\)에서 sample을 가져와 \(x^*\)를 대체한다.
○ Optimal seed sampling
또 다른 디자인 초이스에는 어떻게 majority seed sample \(x_0\)을 고를 것인가에 대한 부분이 있다. Rejection criterion에 따르면 sampling distribution \(Q(k_0|k)\)는 다음의 두 가지 특징을 만족시켜야 한다.
- Q는 rejection criterion에 대해서 acceptance 확률 \(P_{accept}(k_0|k)\)를 최대화 해야 한다: 즉, 유의미한 \(x^*\) 생성을 할 수 있도록 \(k_0\)를 효과적으로 선택해야 한다는 의미이다.
- Q는 최대한 다양한 클래스를 선택할 수 있도록 해야 한다: entropy \(H(Q)\)가 최대화 되어야 한다
이를 만족시키기 위한 optimization problem을 다음과 같이 구성할 수 있다.
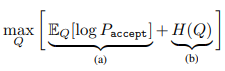
잘 생각해보면 이 수식은 KL divergence와 동일한 형태임을 쉽게 알 수 있다. 따라서 \(Q\)가 \(P_{accept}\)일 때 위의 수식이 최대가 된다. 따라서 저자들은 \(Q\)를 다음과 같이 정하였다.

분포 \(Q\)를 기반으로 \(k_0\)를 선택하면 \(x_0\)는 해당 class의 sample들에 대해서 uniform 분포를 따라 추출을 진행했다고 한다.
완성된 알고리즘은 다음과 같다.

○ Practical implementation via re-sampling
실제로 M2m에서 \(f\)를 학습시킬 때에는 batch-wise resampling을 진행했다고 한다. Balanced dataset을 만들기 위해 어떤 class k에 대해 \(N_1 - N_k\)개의 sample을 생성하고자 하였는데, 이를 batch-wise하게 구현하기 위하여 확률을 도입하였다. Class-balanced mini-batch \(\mathcal{B} = {(x_i, y_i)}^m_{i=1}\)에서 모든 \(i\)에 대해 \( \frac{N_1 - N_{y_i}}{N_1} = 1 - \frac{N_{y_i}}{N_1} \)의 확률로 generation을 진행한다. 여기서 Class-balanced mini-batch \(\mathcal{B}\)는 standard re-sampling 을 통해 얻는다고 한다.
Index \(i\)에 대해 generation을 진행한다고 하면 \(k_0 \in y^m_{i=1}\)을 만족할 때까지 \(k_0 \sim Q(k_0|k) \)을 sampling하고, \(\mathcal{B}\) 내에서 class \(k_0\)의 sample \(x_0\)를 선택한다. 이후 \(x_0\)가 class \(y_i\)가 될 수 있도록 gradient descent 기법으로 optimization을 진행하고, stability를 위해 만들어진 \(x^*\)가 \(\mathcal{L}(g;x^*, y_i)\)가 \(\gamma > 0\)보다 작은 경우에만 이를 활용하여 학습할 수 있도록 한다.
Experiments
○ Experimental setup
CIFAR-10/100, ImageNet-LT, CelebA, SUN397, Twitter, Reuters 데이터셋에 대해 실험을 진행했다. 각 데이터셋별 class-wise sample distribution은 다음과 같다.
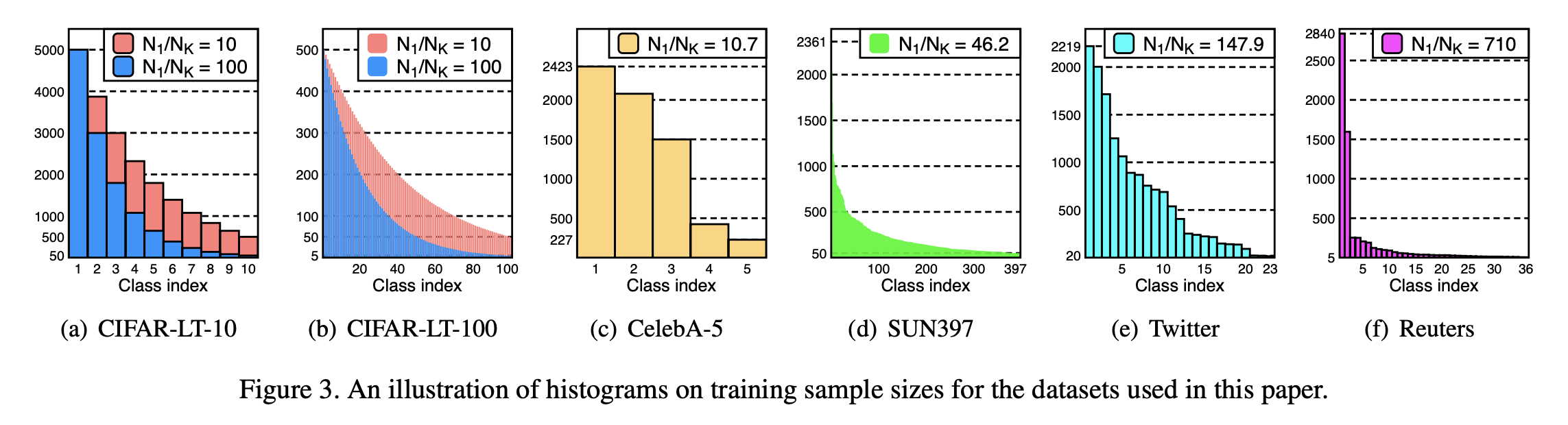
또한 model이 balanced test distribution에 대해 잘 작동하는지를 확인하기 위하여 balanced accuracy (bACC) 와 geometric mean score (GM) 값을 보고하였다. 이 값은 class별 sensitivity (i.e. recall)에 대해 각각 산술, 기하 평균을 의미한다.
Baseline methods
- empirical risk minimization (ERM): re-balancing 없이 cross-entropy loss로 학습
- re-sampling (RS): sampling 확률을 달리하는 방식
- SMOTE: data augmentation을 활용한 re-sampling의 변형 메소드
- re-weighting (RW): sample별로 loss에 미치는 영향을 달리하는 방식
- class-balanced re-weighting (CB-RW): re-sampling의 변형 메소드로, class별로 loss에 미치는 영향을 달리함
- deferred re-sampling (DRS): re-sampling을 training의 후반 stage까지 연기한 뒤 적용
- deferred re-weighting (DRW): re-weighting을 training의 후반 stage까지 연기한 뒤 적용
- focal loss (Focal): 어려운 sample, 즉 minority에 보다 집중하여 학습을 진행할 수 있도록 up-weight
- label-distribution-aware margin (LDAM): minority class에 대해 더 큰 margin을 가질 수 있도록 학습
Details on M2m
Classifier \(g\)는 \(f\)와 동일한 아키텍처를 가지며 standard ERM을 통해 주어진 imbalanced dataset을 학습시킨다. 또한 M2m 메소드는 초반 몇 에폭의 standard ERM 학습을 진행한 뒤 적용하기 시작한다.
○ Long-tailed CIFAR datasets

위의 그림은 CIFAR 데이터셋을 인위적으로 불균등하게 만든 CIFAR-LT-10, CIFAR-LT-100에 대한 실험 결과이다. M2m은 기존의 기술들의 성능을 뛰어 넘는 결과를 보였으며 SOTA로 알려진 LDAM-DRW 또한 능가한다. 또한 M2m을 LDAM에 적용하면 bACC는 더욱 향샹되는 모습을 보인다. 이는 M2m가 LDAM으로부터 얻을 수 있는 학습의 이점과는 다른 축으로의 이점을 취하고 있음을 보여준다.
○ Real-world imbalanced datasets
저자들은 M2m의 효과성을 입증하기 위해 4가지 잘 알려진, 본래부터 불균등한 데이터셋인, CelebA, SUN397, Twitter, Reuter 데이터셋에서도 실험을 진행했다.
- CelebA는 원래 multi-labeled dataset이다. 저자들은 이 데이터셋에서 hair color에 대해 5개의 overlap되지 않는 label을 선정하여 5-way classification 문제로 변형하였다. 또한 imbalance ratio는 유지하면서 전체 데이터셋의 1/20만을 subsample한 뒤 사용함으로써 task를 더 어렵게 만들었다.
- Twitter와 Reuters 데이터셋은 NLP 데이터셋이지만, 더 극심한 불균등 분포 상황에서도 메소드가 효과적인지를 확인하기 위해 실험을 진행했다고 한다. Reuters 데이터셋의 test set에서는 5개 이하의 sample을 가진 class를 제외하여 더 reliable한 평가를 진행하였다고 한다.
- 위와 같이 test set을 구성하는 것이 reliable한지 잘 이해되지는 않았음.

Table 2에서도 M2m이 다른 baseline을 뛰어넘는 성능을 보임으로써, natural imbalance 상황에서도 효과적임을 입증했다. 특히 Reuters 데이터셋에서는 상당한 성능 향상을 보였다. 저자들은 이에 대해 극심하게 데이터가 불균등할 때 M2m 메소드가 더욱 효과적임을 보여주는 것이라고 주장하였다.
○ Ablation Study
추가 실험은 imbalance ratio \(\rho = 100\)인 CIFAR-LT-10 에 대해 진행했다. 또한 majority와 minority class에 대한 balanced test accuracy도 추가적으로 보고하여 두 class에 대한 상대적 영향을 확인하고자 하였다. Majority class와 minority class는 각각 전체 데이터 수의 약 50% 정도를 포함하도록 나누었다.
Diversity on seed samples

각 class 별로 seed sample pool의 크기를 제한했을 때의 성능 변화를 위와 같이 관찰하였다. 결과를 통해서도 알 수 있듯이 seed sample의 다양성이 향상될 수록 minority class의 정확도가 높아지며, 이는 M2m이 majority class의 다양함을 활용하여 minority class에 over-fitting 하는 문제를 방지하는 것으로 볼 수 있다고 한다.
- minority class의 정확도를 Table 3에서는 따로 report하지 않았는데, 어떻게 위와 같이 주장할 수 있는지 의문이 든다.
The effect of \(\lambda\)
저자들은 \(x^*\)를 생성하기 위한 optimization problem에서 regularization term \(\lambda \cdot f_{k_0}(x) \)을 통해 synthetic sample의 질을 향상시킬 수 있다고 주장한다: 만약 생성된 sample이 여전히 original class의 중요한 feature를 포함하고 있다면 \(f\)를 혼란시키게 된다.

Table 4에서 \(\lambda\)를 0으로 한 실험 결과를 살펴보면 M2m에 비해 성능이 하락이 있음을 알 수 있다.
Over-sampling from the scratch
M2m은 초반 몇 에폭을 지난 뒤부터 메소드를 적용하기 시작하는 "deffered" scheduling 전략을 사용한다. 이 전략을 사용하지 않은 방식을 M2m-RS라고 하였다. 이에 대한 결과 또한 Table 4에서 확인할 수 있다. M2m-RS가 Table 1에 보고된 다른 baseline의 성능을 여전히 능가하고 있지만 기존의 M2m보다는 약간의 성능 하락이 있다.
Labeling as a targeted class
Pre-trained classifier \(g\)도 minority class에 대해 generalizable한 이상적인 classifier가 아니기 때문에, \(g\)를 활용하여 생성한 \(x^*\) 또한 target minority class의 generalizable feature를 잘 포함하고 있다고 결론지을 수 없다.
\(x^*\)가 얼마나 target class에 잘 연관되어 있는지를 확인하기 위해 M2m-RS-Rand를 진행했다. 이는 M2m-RS에서 \(x^*\)를 target class로 labeling 한 것과 달리, random class로 labeling을 한 결과이다. 결과는 마찬가지로 Table 4에서 확인할 수 있다. M2m에 비해 Minority class에서 성능 하락이 발생하는 것으로 미루어 보아 알맞게 labeling된 synthetic data가 minority class에 대한 일반화 능력을 향상시킨다고 볼 수 있다.
- Random 뿐만 아니라 original class로 재 labeling한 결과도 확인할 수 있었으면 더 좋았을 것 같다고 생각한다.
Comparison of t-SNE embeddings
t-SNE를 활용하여 마지막 feature space를 시각화하였다.

이는 CIFAR-LT-10 데이터셋에서 각 class 별로 50개의 saple을 random하게 추출하여 나타낸 embedding이다. 이를 통해 M2m이 다른 메소드에 비해 비교적 잘 구분되는 feature를 만들고 있음을 확인할 수 있다.
Comparison of cumulative false positive

Figure 5에는 false positive (FP)의 수를 그래프로 나타내었다. 여기서 \(FP_k\)는 test set에서 k class로 잘못 예측된 sample의 수를 의미한다. 그래프는 majority class부터 class index를 따라 cumulative하게 합산하여 나타내었다. 잘 학습된 이상적인 classifier는 linear한 그래프를 가질 것이다: 각 클래스들에 대하여 균등하게 실수를 한다. Figure 5에서 알 수 있듯이 M2m을 활용한 메소드는 다른 메소드들에 비해 비교적 FP를 적게 만들고 있으며, 보다 linear한 형태를 띄고 있으므로 imbalacned learning에 바람직한 특성을 가지고 있다고 판단할 수 있다.
The use of adversarial examples
M2m의 생성 과정은 종종 synthetic minority sample가 original sample과 유사한 형태로 남은 채로 종료되기도 한다. 이는 adversarial example과 비슷하게 생각할 수 있다. 이에 대한 예시는 다음의 Figure 6을 통해 살펴볼 수 있다.

Adversarial perturbation이 M2m에 어떻게 영향을 미치는지 살펴보기 위해 M2m-Clean이라는 실험을 진행했다. 이는 \(x^*\) 대신 clean한 \(x_0\)를 사용한 것으로 단순 over-sampling을 진행한 형태이다. Table 4를 보면 동일한 실험 환경인데도 M2m에 비해 상당한 성능 하락이 있는 것을 확인할 수 있다. 이는 adversarial perturbation이 small noise 이지만 굉장히 중요한 역할을 하고 있다는 것을 보여주는 실험 결과이다.
Conclusion
- Imbalanced classification 문제를 위해 Major-to-minor Translation (M2m)이라는 새로운 over-sampling 메소드를 제안함
- Majority class의 다양성이 데이터 불균등 환경에서 도움을 줄 수 있음을 확인함
- Adversarial perturbation이 imbalanced learning에서 효과적일 수 있음을 보임
- 이 연구가 imbalanced learning과 adversarial example 연구의 새로운 방향이 되기를 바람